2.1 이산 분포

표본 공간 S를 사용한 무작위 실험에서 s가 S의 실수에만 해당하는 함수 X는 함수 X입니다. f(x)는 무작위 변수입니다.
X의 공간은 실수 집합이며, 여기서 X(s)=x이고 s는 S의 요소입니다. ‘s는 S의 원소이다’의 의미는 s가 집합 S에 속한다는 것을 의미합니다.
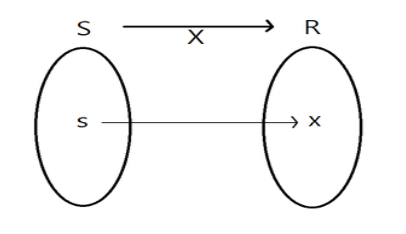
고등학교에서 배운 함수의 정의로 영역은 영역과 1:1로 대응된다. 여기서 도메인을 패턴 공간으로 생각할 수 있습니다.
즉, 랜덤 변수는 함수입니다.
정의 2. pmf(확률 질량 함수)
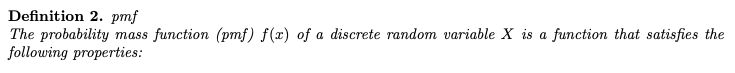
이산확률변수 X에 대한 확률질량함수 pmf는 다음 성질을 만족하는 함수이다.
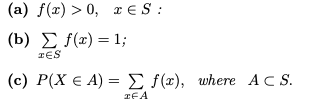
1. 도메인 x가 S의 요소라고 가정하면 f(x)는 0보다 큽니다.
2. 샘플 공간 S의 x 요소 집합인 영역에 대한 f(x)의 합은 1입니다.
3. X가 A의 원소일 확률은 A의 x 원소에 대한 f(x)의 합과 같습니다. 그러나 A는 S의 부분집합입니다.
누적 분포 함수(cdf)의 정의

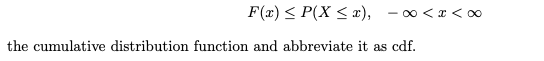
누적 분포 함수는 다음과 같습니다. cdf로 약칭.!
Ex 불연속 균일 분포 (이산 등분포)

육면체 주사위를 던지는 무작위 실험을 상상해 보십시오. 이 실험의 표본 공간은 S={1,2,3,4,5,6}이고 S의 요소는 위에 표시된 점의 수를 나타냅니다.
이 경우 X는 S에서 불연속 균일 분포를 가지며 pmf(확률 질량 함수)는 다음과 같습니다.
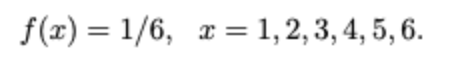
그리고 cdf는
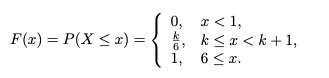
이것은 k 값에 따라 다릅니다.
예 2.1-4

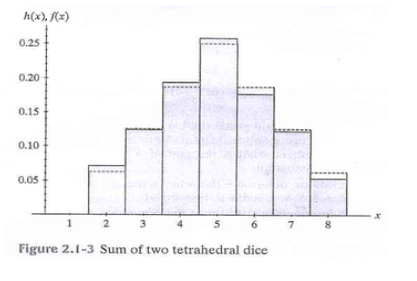
패턴 필드가 1, 2, 3, 4인 직선 사면체 주사위를 두 번 던집니다. X를 두 결과의 합과 같게 합니다.
X에 가능한 값은 2.3,…,8입니다. 이 실험은 컴퓨터에서 1000번 시뮬레이션되었습니다. 표 2.1-1은 결과 목록이며 해당 확률을 상대 빈도와 비교합니다.
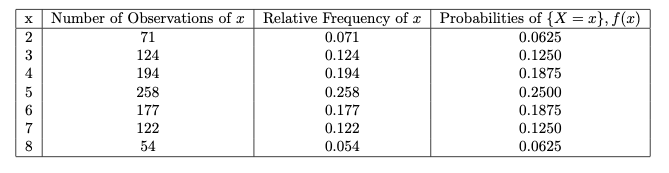
다음은 확률 함수 f(x)의 히스토그램입니다. 그림 면적의 합은 1입니다.
2.2 수학적 기대치

확률 함수 f(x)가 X 샘플 공간 S를 갖는 이산 X의 확률 질량 함수라면,
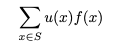
존재하는 경우 이들의 합을 u(x)의 수학적 기대값 또는 u(x)의 기대값이라고 합니다.
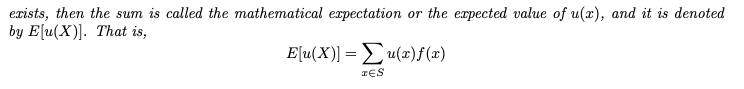
예제 2.2-2
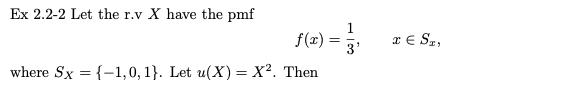
확률 변수 X가 확률 질량 함수 pmf를 갖고 다음을 따른다고 가정합니다.
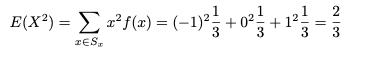
정리 1. – 기대 속성
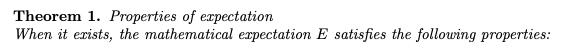
수학적 기대값 E가 존재하는 경우 E는 다음 속성을 충족합니다.

a) c가 상수이면 Ec = c
b) c가 상수이고 u가 함수이면 E(cu(X)) = cE(u(X)).
c) c_1과 c_2가 상수이고 u_1과 u_2가 함수라면 위와 같다.
그것을 증명합시다.
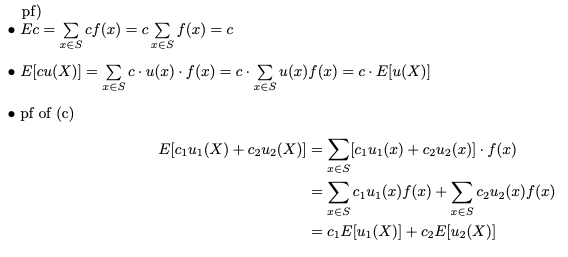
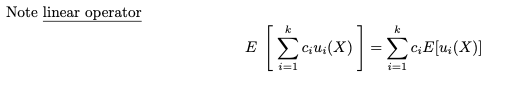
즉, 수학적으로 기대되는 값 E는 선형입니다.
예제 2.2-3
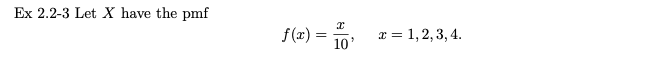
X는 확률 질량 함수를 가지므로 X의 평균은
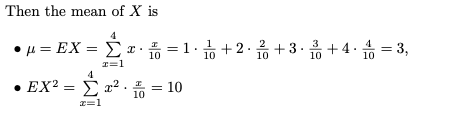
예제 2.2-4

u(x)라고 하자. 여기서 b는 X의 함수가 아니다. 다음과 같은 기대값이 존재한다고 가정하고 위의 기대값을 최소화하는 b의 값을 찾는다.
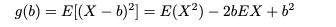
최소값을 찾기 위해 b에 대해 g(b)를 미분하고 g'(b)=0에 대해 풉니다. 그 다음에
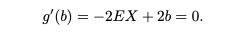
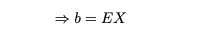
g”(b) = 2 > 0이므로 X의 평균 EX는 위의 기대치를 최소화하는 b의 값입니다.
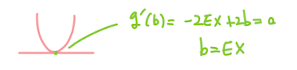
Ex 2.2-5 기하학적 분포
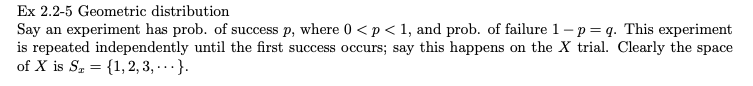
실험을 해보세요. 성공은 p, 실패는 1-p = q입니다. (0
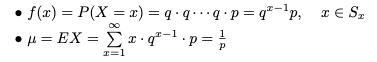
2.3 특별한 수학적 기대치

- 분산은 mu에 대한 2차 모멘트의 결과입니다.
- 평균에 대한 1차 모멘트는 0입니다. (계산하면 나온다)
정의 4. 메모리 생성 기능
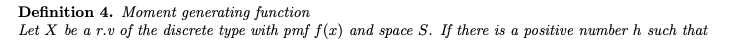
X를 표본 공간 S와 확률 질량 함수 f(x)를 갖는 이산 확률 변수라고 합니다. 유한한 경우 -h < t < h(h는 양수임)
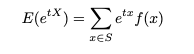
가능한 경우

M
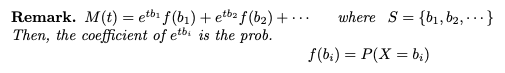
e^tb_i의 계수 f(b_i)는 확률 함수입니다.
즉, 위의 상황에서 S = {b_1, b_2, …, b_n}이다.
순간발생함수의 고유성(mgf)

두 확률 변수의 mgf가 같으면 확률 분포가 같아야 합니다.
두 확률 변수 f(x)와 g(y)가 두 개의 확률 질량 함수로 동일한 표본 공간 {b_1,b_2, …}을 가지면 모든 t에 대해 동일한 모멘트 생성 함수를 얻을 수 있기 때문입니다.
즉, 수학적 변환 이론에 따르면 다음과 같은 방정식이 인식됩니다.
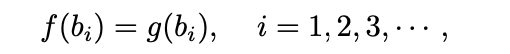
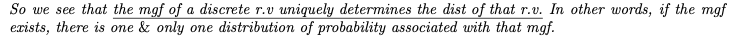
랜덤 변수의 분포는 이산 랜덤 변수의 모멘트 생성 함수에 의해 고유하게 결정된다는 것을 알고 있습니다.
예제 2.3-7
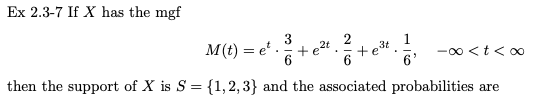
X가 위의 mgf(모멘트 발생 함수)를 갖는다면 XS = {1, 2, 3}의 지지(도메인)와 그에 따른 확률은 다음과 같다.
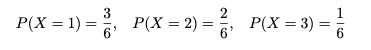
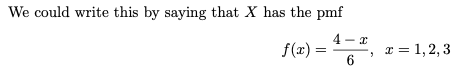
X에 확률 질량 함수가 있다고 가정하면 확률 함수는 다음과 같이 쓸 수도 있습니다.
예제 2.3-8
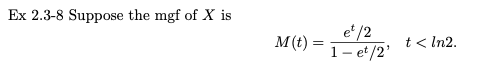
X의 모멘트 생성 함수가 다음과 같다고 가정합니다.
이러한 적률 생성 함수를 이용하여 확률변수 X의 확률질량함수를 즉시 상기하는 것은 쉽지 않다.
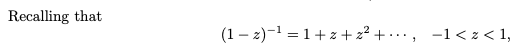
우리가 과거에 배웠던 Taylor 확장을 고려하십시오. 이를 통해
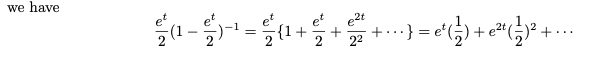
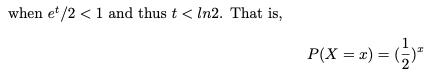
다음과 같은 X의 확률 질량 함수를 찾을 수 있습니다.
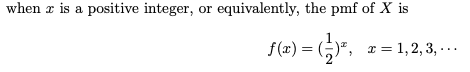
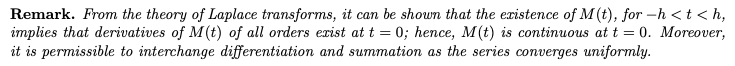
라플라스 변환 이론에서 우리는 M

예제 2.3-9
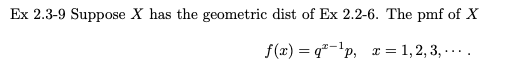
X가 예제 2.2-6의 기하학적 분포를 갖는다고 가정합니다. 그러면 X의 확률 질량 함수는 위와 같습니다.
그렇다면 X의 모멘트 생성 기능은 무엇일까요?
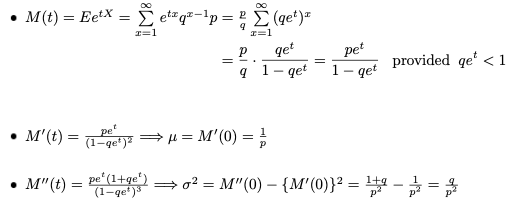
2.4 이항 분포 (이항분포)
정의 5. 베르누이 실험

Bernoulli 시행은 결과가 상호 배타적이고 성공 또는 실패로 완전히 분류될 수 있는 무작위 실험입니다.
정의 6. 일련의 Bernoulli 실험
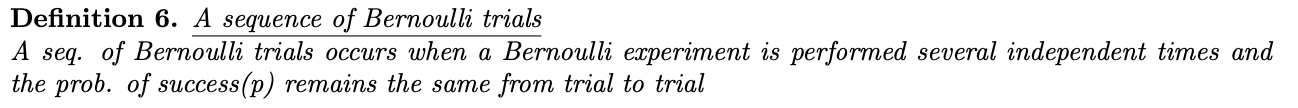
연속 베르누이 시행은 베르누이 시행이 독립적으로 여러 번 수행될 때 발생합니다. 성공 확률은 각 시도에서 동일하게 유지됩니다.
예제 2.4-1

사탕무 종자의 발아율은 0.8로 높고 종자의 발아는 성공했다고 한다. 10개의 종자를 심고 한 종자의 발아가 독립적이라고 가정하면 다른 종자의 발아율은 확률 p가 0.8인 베르누이 시행 10회와 동일합니다.
정의 7. 베르누이 거리(베르누이 분포)

X를 다음 정의의 Bernoulli 시행과 관련된 랜덤 변수라고 합니다.
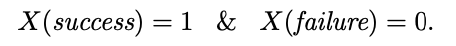

그러면 X의 확률 질량 함수는 다음과 같습니다. 그리고 우리는 이 X가 베르누이 분포를 갖는다고 말할 수 있습니다.
예제 2.4-4
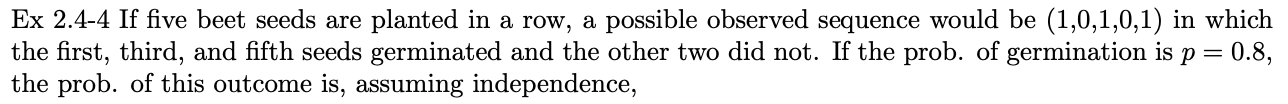
5개의 사탕무 종자를 일렬로 심으면 관찰 가능한 순서는 (1,0,1,0,1)이고, 1, 3, 5번째가 발아하고 나머지 2개는 죽었다. 발아 성공률이 0.8이고 확률이 독립적이라고 가정하면 결과의 확률은 다음과 같습니다.
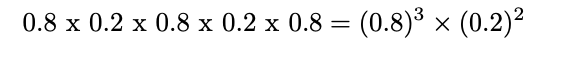
정의 8. 이항 분포
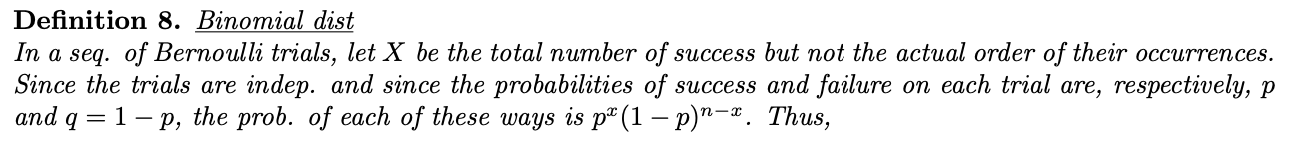
한 줄의 X를 실제로 발생한 순서가 아니라 Bernoulli 시행의 총 성공 횟수라고 합니다.
각 시도는 독립적이고 성공과 실패의 확률은 각각 p와 q = 1-p이므로 이 사건의 확률은 위와 같습니다. 그런 다음 이러한 이벤트의 확률 함수를 다음과 같이 표현할 수 있으며 이 X가 이항 분포라고 말할 수 있습니다.
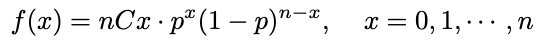
n번 시행 중 x번 시행은 언제 발생하는지는 중요하지 않으므로 베르누이 시행 전에 조합을 추가하는 것이 포인트입니다.
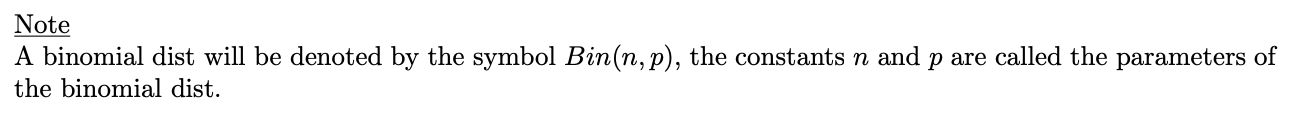
예제 2.4-5

당첨 확률이 20%인 즉석 복권의 경우 n번 구매 중 당첨된 숫자를 X라고 합니다. 두 장의 복권을 살 확률은 다음과 같습니다.
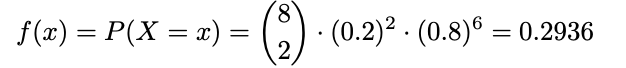
예제 2.4-7
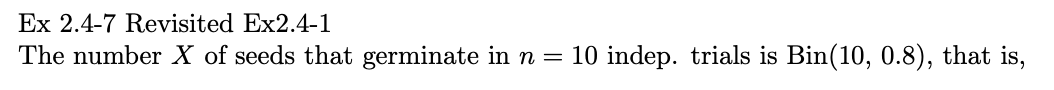
X가 10번의 독립적인 시도에서 발아된 종자의 수인 경우 해당 시도는 10번의 시도에 대한 성공 확률이 0.8인 이항 분포입니다. 그러면 확률 함수는 다음과 같습니다.
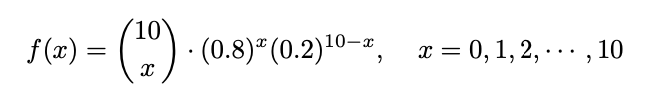
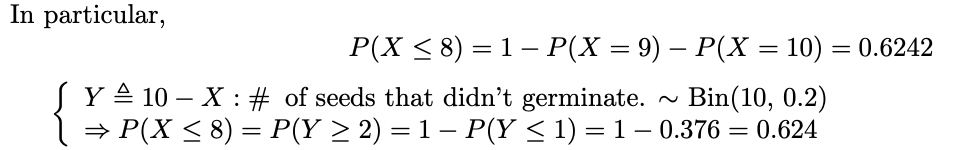
P(X<=8) ist gleich der Wahrscheinlichkeit, dass P(Y>=2) 씨앗이 2개 미만인 씨앗은 발아하지 않습니다.
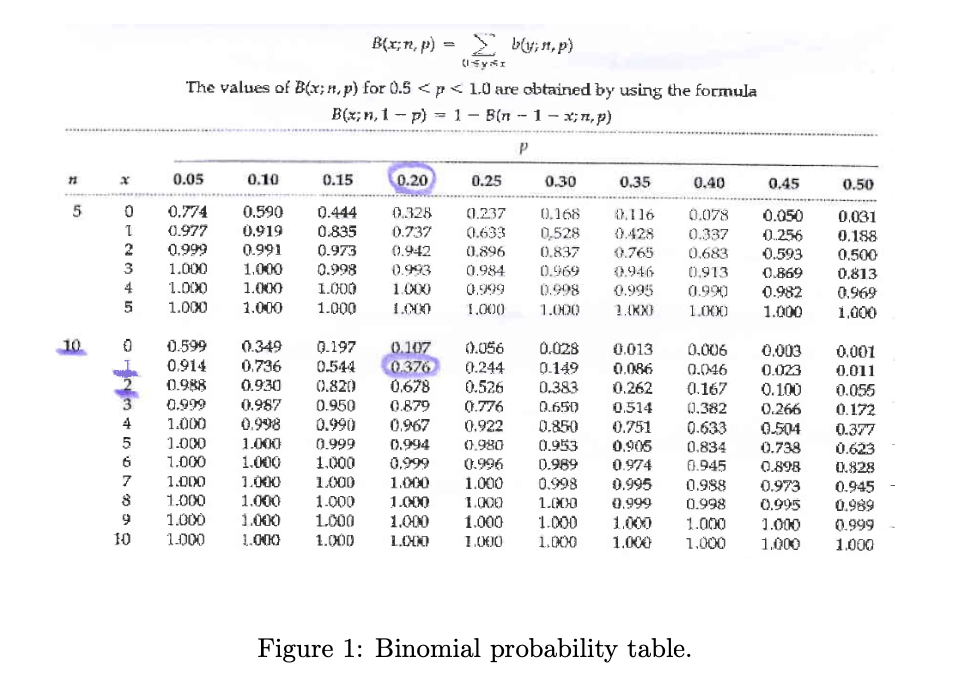
주석. 이항 분포의 mgf(이항 분포의 적률 생성 함수)
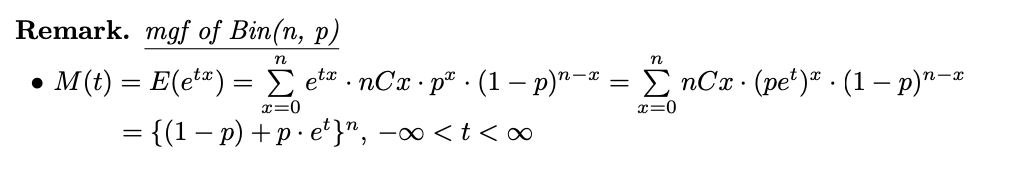
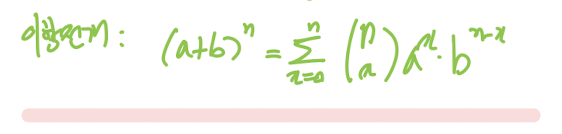
주석. Bin(n,p)의 평균과 분산
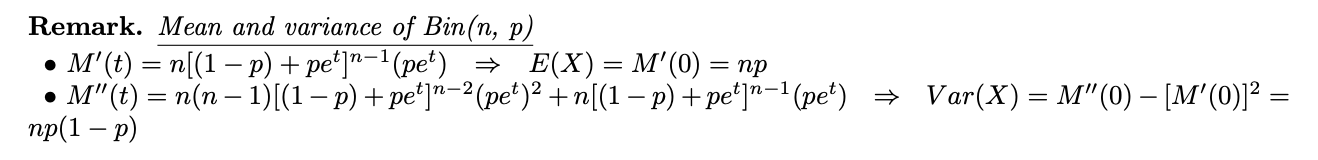
2.5 초기하 거리 (초기하 분포)

유사한 객체 N_1 및 N_2 세트를 고려하십시오. N_1은 이분법적 클래스 중 하나인 레드 칩이고 N_2는 또 다른 클래스인 블루 칩입니다. n개의 개체 집합(여기서 n은 1보다 크고 N_1+N_2보다 작거나 같음)이 선택되었으며 N개의 개체가 교체 없이 무작위로 추출되었습니다. X를 첫 번째 클래스가 선택된 객체의 수라고 합니다. 양의 정수 x는 n,N_1보다 작거나 같고 nx는 N_2보다 작거나 같다고 가정합니다. 그러면 n개의 객체 중 x개는 첫 번째 클래스에 속하고 nx개의 객체는 두 번째 클래스에 속할 확률이 있습니다.
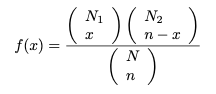
예제 2.5-2
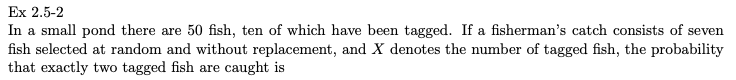
50마리의 물고기가 있는 작은 연못에 10마리가 표시되었습니다. 어부의 어획물이 강화 없이 무작위로 선택된 7마리의 물고기로 구성되고 X가 표시된 물고기의 수를 나타낸다면 표시된 물고기가 정확히 2마리 잡힐 확률은
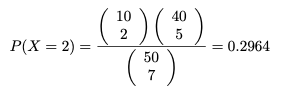

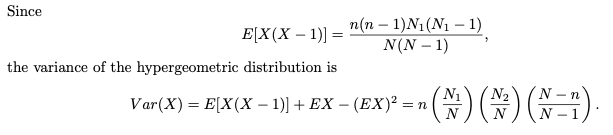
초기하 분포의 평균과 분산에 대하여 유도해보자.
주석. 이항 및 초기하 분포
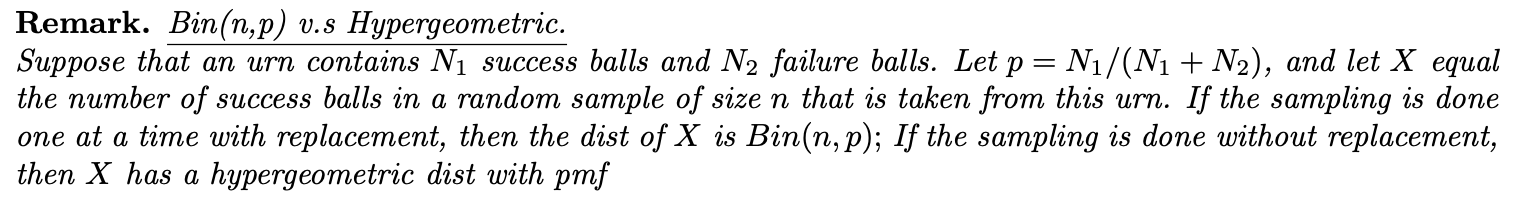
팟에 N_1개의 히트 볼과 N_2개의 실패 볼이 있다고 가정합니다. p N_1/(N_1+N_2)라고 하고 X는 이 항아리에서 무작위로 추출한 크기 n의 성공한 공의 수라고 합니다. 만약 이 추출이 치환으로 수행된다면 X의 분포는 이항분포가 될 것이고, 이 추출이 치환 없이 수행된다면 X는 확률질량함수를 갖는 초기하 분포를 갖게 될 것입니다.
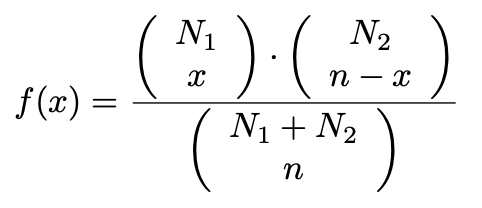
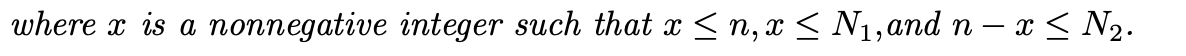
여기서 x는 음이 아닌 정수이며 위와 동일한 조건을 가집니다.
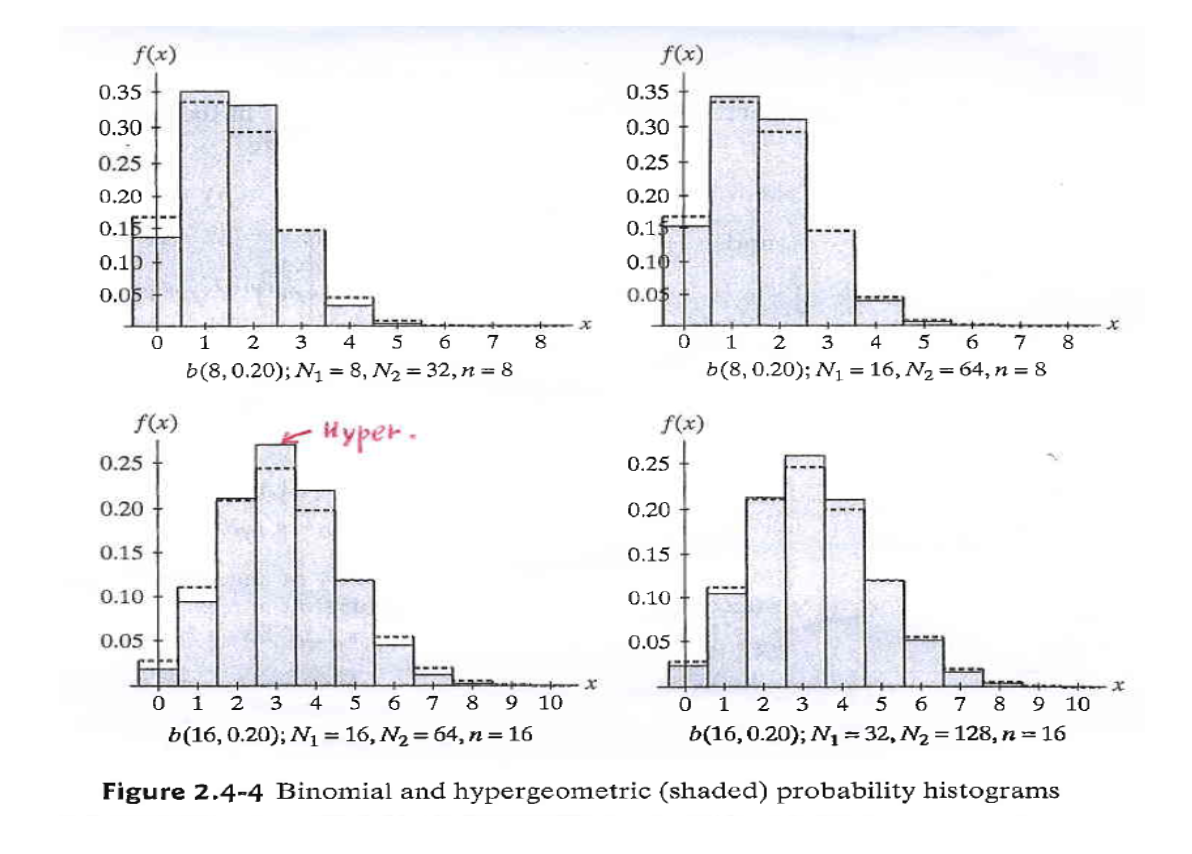
위의 그림에서 우리는 n이 고정되었을 때 N의 크기가 확률에 미치는 영향을 관찰할 수 있습니다.
2.6 음의 이항 분포
정의 9. 음의 이항분포
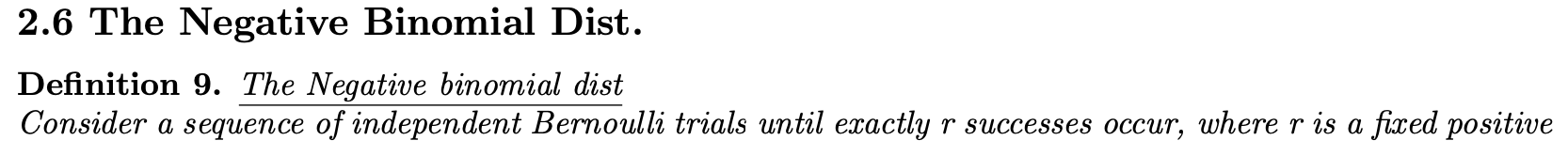
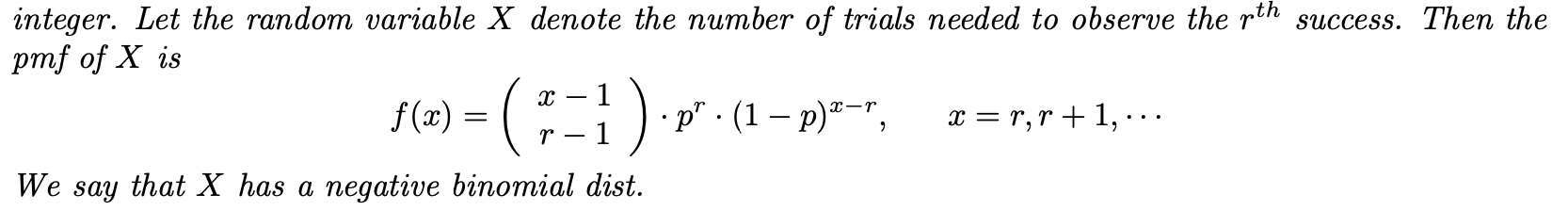
r번째 성공이 발생할 때까지 연속 베르누이 시행을 수행한다고 가정합니다. 여기서 r은 고정된 양의 정수입니다. X를 관찰할 r번째 성공에 필요한 시행이라고 합니다. 그러면 X에 대한 확률 질량 함수는 다음과 같습니다. 여기에 X가 있습니다. 음이항분포가지고 있다고 말하다
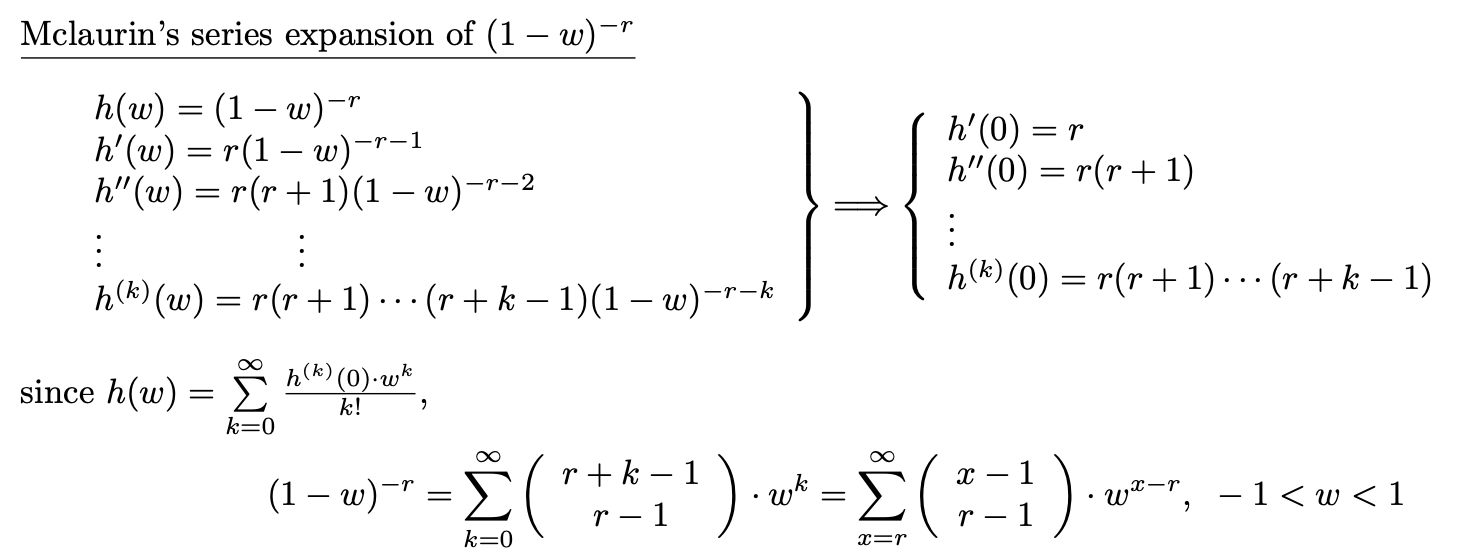
Maclaurin 시리즈를 확장하면 다음을 얻습니다.
예제 2.6-1

생물학 학생들은 다수의 초파리의 눈 색깔을 확인했습니다. 개별 파리에 대한 확률을 가정합니다. 하얀 눈의 확률은 1/4이고 빨간 눈의 확률은 3/4입니다. 이 시점에서 우리는 이러한 관찰을 독립적인 Bernoulli 실험으로 취급할 수 있습니다. 가루이를 관찰하기 위해서는 파리의 적어도 네 개의 눈을 검사해야 합니다.
음이항 분포의 적률 생성 함수
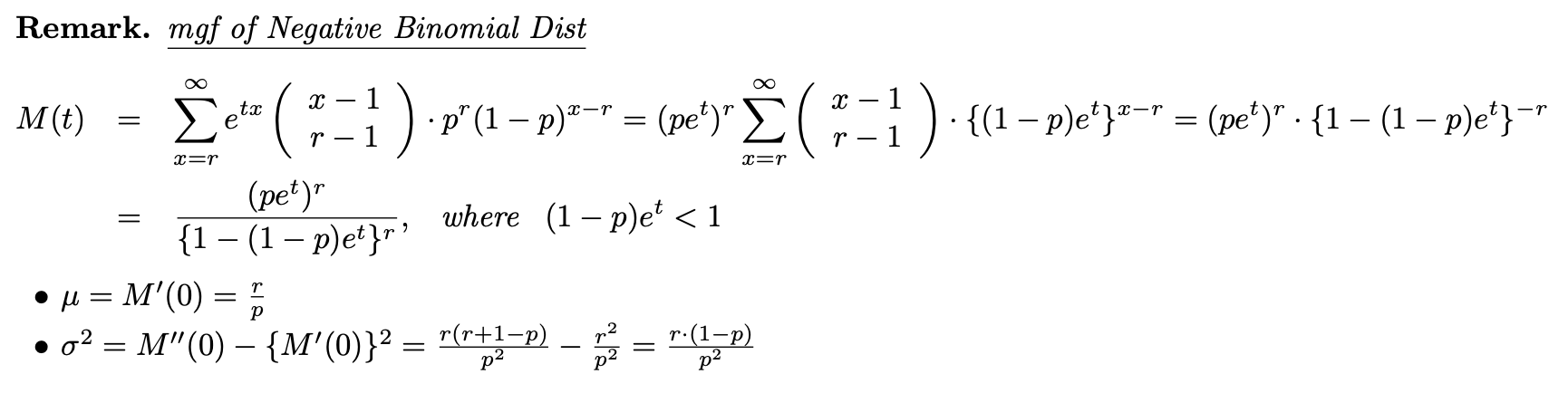
예제 2.6-2

농구 선수가 연습 중 자유투 성공률이 80%라고 가정합니다. 우리는 연속적인 자유투가 독립적이라고 계속 가정합니다. 그렇다면 이 경우는 베르누이 과정이 될 것입니다. X는 이 선수가 10골을 넣기 위해 시도해야 하는 최소 자유투 수입니다. 그러면 X의 확률 질량 함수는 다음과 같습니다.
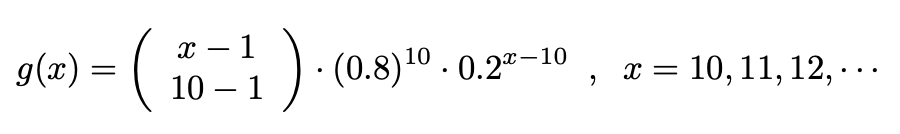
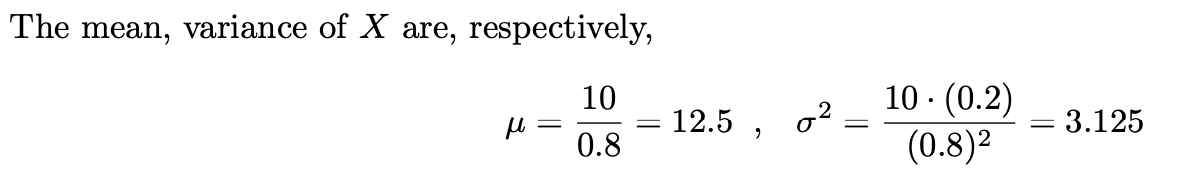
평균과 분산은 위와 같습니다.
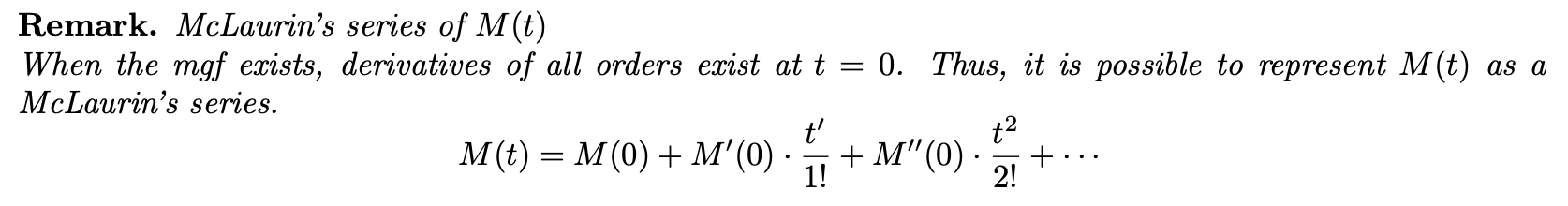
모멘트 생성 함수가 존재하면 모든 도함수는 t = 0에서 존재합니다. 따라서 M
예제 2.6-4
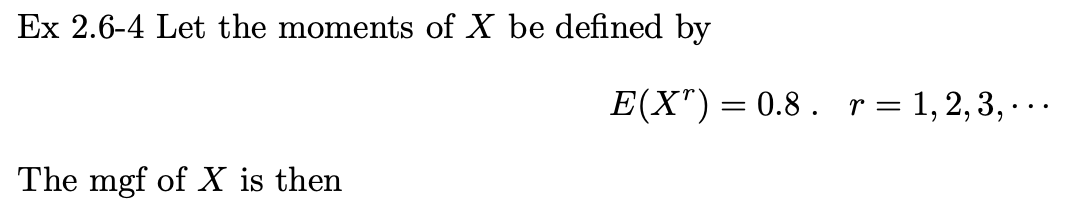
X의 모멘트를 다음과 같이 정의합니다. 다음은 X의 모멘트 생성 함수입니다.
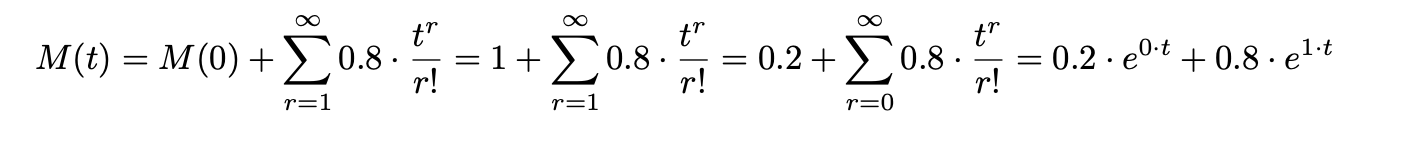
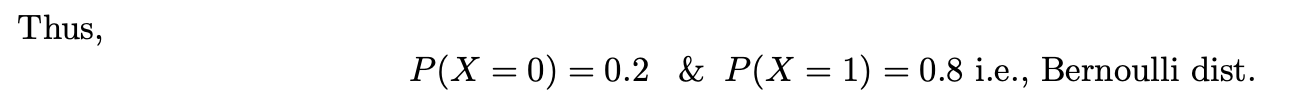
따라서 P(X=0) = 0.2 & P(X=1)=0.8인 베르누이 테스트입니다.
예제 2.6-5

각 면이 적어도 한 번은 관찰될 때까지 곧은 6면체 주사위를 굴립니다. 평균 몇 롤을 굴려야 합니까? 첫 번째 결과를 관찰하려면 항상 결과가 필요합니다. 첫 번째 롤과 다른 쪽을 관찰하는 것은 p가 5/6이고 q가 1/6인 기하학적 랜덤 변수를 관찰하는 것과 같습니다. 따라서 평균적으로 6/5를 굴려야 합니다. 다른 두 얼굴을 관찰한 후 새로운 얼굴이 관찰될 확률은 4/6입니다. 따라서 평균적으로 6/4번 굴려야 합니다. 이 방법을 계속하면 답은 다음과 같습니다.
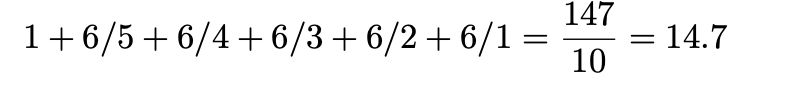
2.7 푸아송 분포 푸아송 분포.
정의 10. 포아송 프로세스

주어진 이벤트 시퀀스에서 이벤트가 여러 번 발생합니다. 간격이 계산됩니다. 그러면 이벤트가 다음 조건을 만족하고 람다가 0보다 크면 근사 포아송 과정을 가집니다.
a) 겹치지 않는 하위 구간의 발생 횟수는 독립적입니다.
b) 길이가 h인 충분히 짧은 하위 구간에서 발생하는 확률은 lambda*h에 접근합니다.
c) 충분히 짧은 하위 구간에서 두 개 이상의 사건이 발생할 확률은 본질적으로 0입니다.
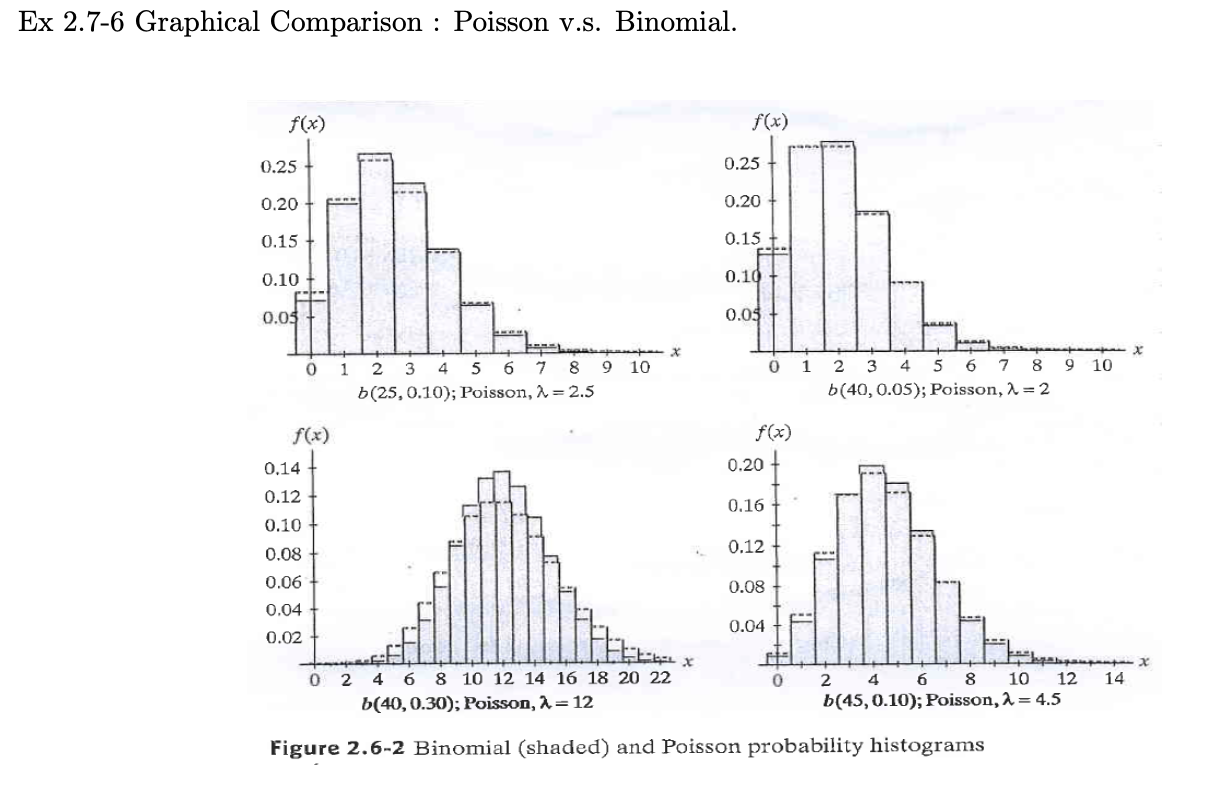
포아송 분포와 이항 분포의 비교

실험이 근사 포아송 과정의 세 가지 조건을 만족하는 경우 X는 길이 1의 구간에서 발생하는 사건의 수를 나타냅니다. 음수가 아닌 정수 x에 대해 P(X=x)의 근사치를 찾고자 합니다. 이를 위해 동일한 길이 1/n을 길이 n의 하위 구간으로 세분합니다. n이 충분히 크면 이벤트가 단위 간격에서 x번 발생할 확률을 n개의 하위 구간 중 x개의 하위 구간에서 각각 정확히 하나의 이벤트가 발생할 확률로 근사할 수 있습니다. 조건 b)에 따르면 길이 1/n의 하위 구간에서 사건이 발생할 확률은 대략 람다*(1/n)입니다. 임의의 하위 구간에서 두 개 이상의 사건이 발생할 확률은 본질적으로 0(by c)이며, 각 하위 구간에서 베르누이 시행으로 사건이 발생하거나 발생하지 않는다는 점을 고려하면, 확률은 대략 람다 & (1/n)과 같습니다.
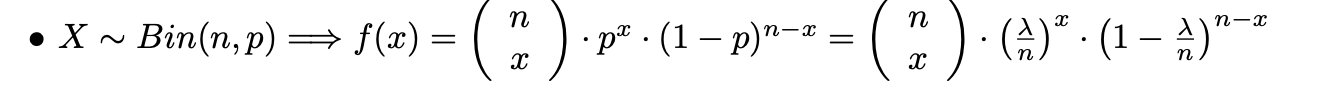
이항 확률에 의해 다음과 같이 주어진다.
푸아송 분포의 pmf
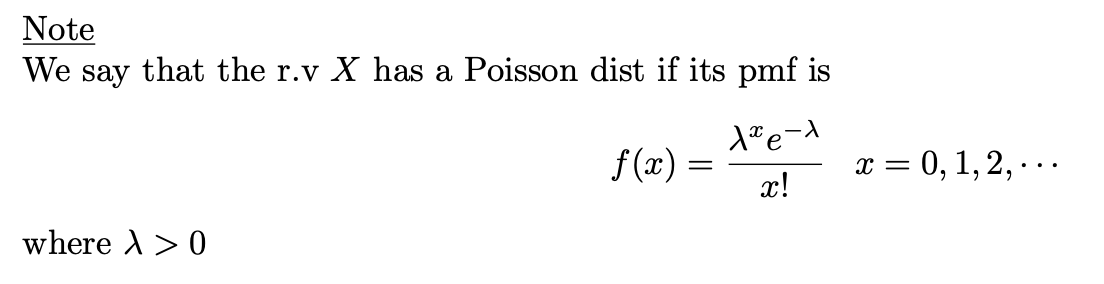
mgf 푸아송 분포
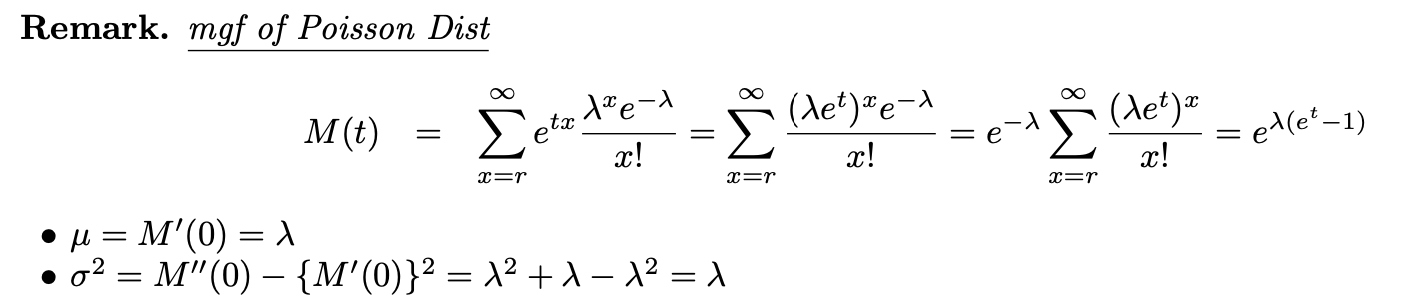
예제 2.7-3

USB 플래시 드라이브는 종종 컴퓨터 파일을 백업하는 데 사용됩니다. 그러나 과거에는 컴퓨터 테이프가 신뢰할 수 없는 백업 시스템으로 사용되었습니다. 그리고 이 테이프에 결함이 나타나기 시작했습니다. 특정 상황에서 중고 컴퓨터 테이프의 평균 결함은 1,200피트당 1개였습니다. 포아송 분포를 가정할 때 X의 분포와 4800피트 롤의 결함 수는 얼마입니까?
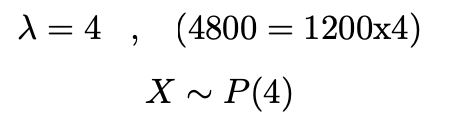
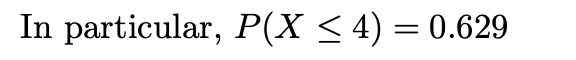
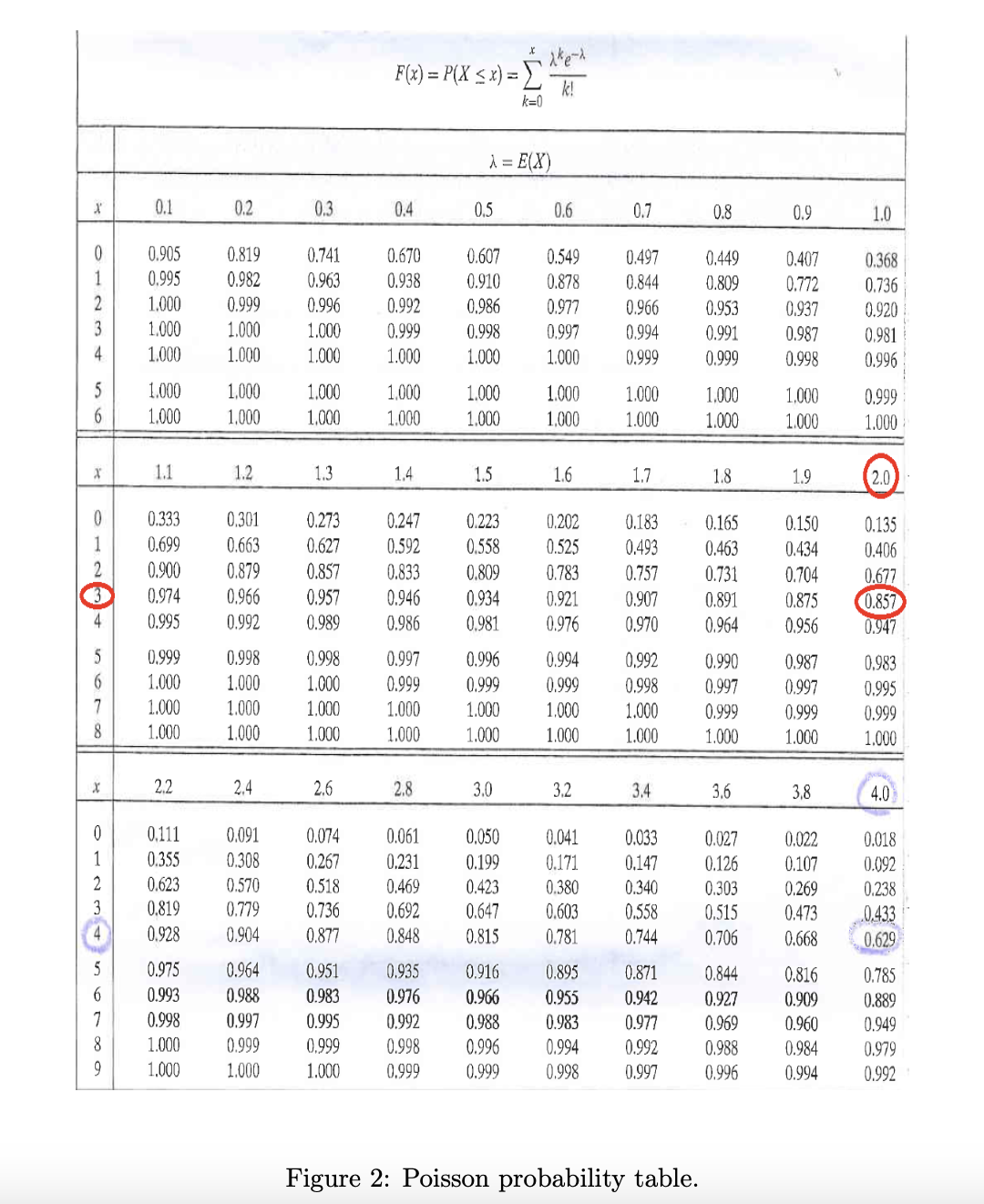
예제 2.7-5
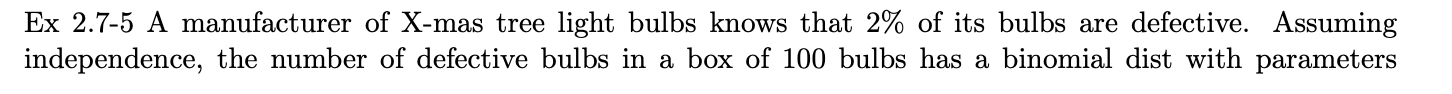

크리스마스 조명 제조업체는 제품의 2%에 결함이 있다는 것을 알고 있습니다. 독립성을 가정하면 램프 100개가 들어 있는 상자의 불량 램프 수는 매개변수 n = 100 및 p = 0.02인 이항 분포를 갖습니다. 확률을 근사화하기 위해 100개의 전구 상자에 최대 3개의 불량 전구가 포함되므로 람다 100*0.02의 푸아송 분포를 사용할 수 있습니다. 이항분포를 이용하면 다소 복잡한 방정식을 통해 다음과 같은 확률을 도출할 수 있다.

통계 패키지 및 통계 계산기의 가용성으로 인해 이항 분포에서 확률을 더 쉽게 계산할 수 있습니다. 따라서 확률을 정확하게 찾을 수 있으면 이항 확률을 계산하기 위해 푸아송 근사를 사용할 필요가 없습니다.